pythonで機械学習をいろいろいじっているのですが、そもそもpython初心者なのでいろいろ難儀しています。
配列の扱い方がさっぱりわかりません。たぶん、覚えればすごく便利なのだと思うのですが、pythonの配列とnumpiがごっちゃになってしまってなかなか整理がつきません。
というわけで、勉強もかねて、以前から気になっていたボリンジャーバンドの検証をしてみようかと思います。
環境
Anaconda3(Jupyter notebook)
python3.5
ライブラリ
numpy,pandas,quandl,matplotlib など
目標
そもそもボリンジャーバンドというのは何かというと、
トレンド系のテクニカル指標。考案者はジョン・A・ボリンジャー (John A. Bollinger)。一般には逆張りに分類されることが多いが、ボリンジャーは順張りに使用している。「Bollinger on Bollinger Bands」(ISBN 0071373683)、「ボリンジャー・バンド入門」(ISBN 4939103536)にて、利用法が紹介されている。
ボリンジャーは1980年代に発表。ただし、平均+誤差の標準偏差という考え方は金融の世界に大昔からある。例えば、1973年に発表されたブラック・ショールズ方程式もこの考え方に基づいている。
算出方法は、
ボリンジャーバンド = x日の移動平均 ± x日の標準偏差 × y
yとしては、2が使われることが多い。移動平均は、単純移動平均が使われることが多いが、単純以外も使われることがある。単純以外を使用する場合は、標準偏差ではなく、移動平均に対する誤差の二乗平均平方根となる。
背後にある理論としては、値動きの正規分布を前提としている。線形自己回帰移動平均モデルと同じ考え方に基づいている。ただし、現実としては、平均からの誤差は正規分布から大きく離れた分布となる。そのため、あくまでも、ボラティリティを測る尺度として、誤差の二乗平均平方根が使われているに過ぎない。正規分布ではないことは、経済物理学を参照。
投資判断は、トレンドが出ているときは終値が上のバンドを上抜いたら買い、下のバンドを下抜いたら売り。レンジ相場のときは逆パターンに利用される。
wikiより引用
下記は、日経平均のボリンジャー・バンドです。
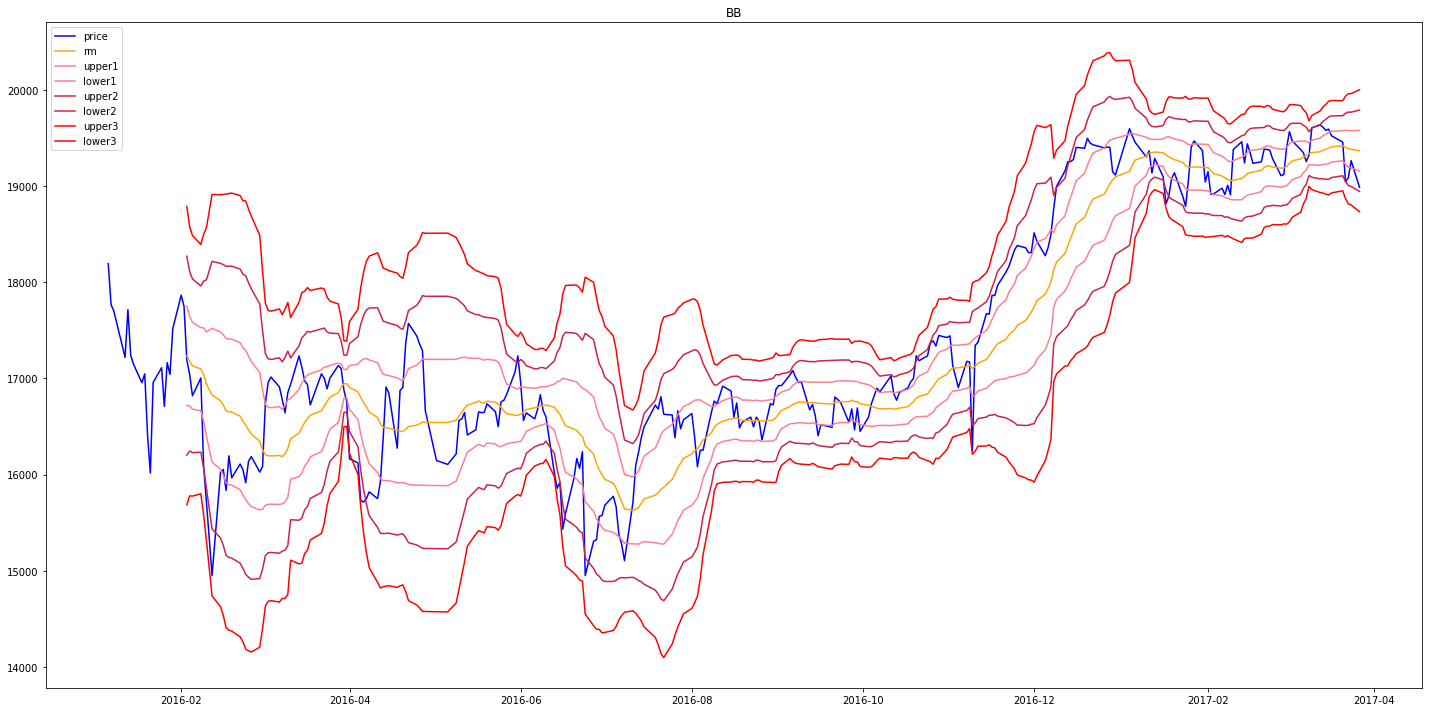
Fig.1
約1年間分の動きをグラフ化しました。
青がその日の終値でオレンジが移動平均線です。終値はほぼ移動平均線に沿って動いています。
その外側の上下に3本ある赤っぽいラインがボリンジャーバンドです。
統計学的に移動平均線(オレンジ色)の
一番近い上下線の間で株価が動く確率(1次標準偏差、1σ)=約68.3%
二番目の上下線の間で株価が動く確率(2次標準偏差、2σ)=約95.5%
三番目の上下線の間で株価が動く確率(3次標準偏差、3σ)=約99.7%
の確率で終値は上記の範囲内にあるだろうという理論です。
極端なことを言えば3番目の下の赤ラインのところを超えたタイミングで買えば、99.7%勝てる!という理論です。
実際に、パッと見、青い線(終値)が赤線(3σライン)に接近することはまれで、交わったところですぐ反発し値上がりしているように見えます。
2016年11月頃にがくんと落ち込んでいる日(※アメリカ大統領選の日ですね)がわかりやすいと思います。
が、じゃあ下のσ3と交わったところで買えばいいじゃん(=逆張り)となるわけですが、実際はそう簡単ではなく、2016年4月とか2016年6月中旬ごろのように一度σ3と接した後、ずるずるとしばらく値下がりする場合もあるので、この状態から値上がりするタイミング(=順張り)の指標として使うばあいもあるようです。
ボリンジャーバンド自体は、大体どこの証券会社でも表示をサポートしていますが、実際に上記の確率の範囲内なのかはわかりませんので、実際に計算してみようというのが今回の趣旨で、ついでにmatplotlibでグラフの表示も試してみようというのが今回の趣旨です。
ソースコード
データの読み込み
データについては日経平均を使いました。
有料、無料含めいろいろ入手方法はありますが、今回はquandlを使いました。
https://www.quandl.com/
なんとAPIも用意してくれていますので
pip install quandl
とするだけで使えます。
実際にはこんな感じ。
import numpy as np
import pandas as pd
import quandl
import matplotlib.pyplot as plt
%matplotlib inline
df = quandl.get('NIKKEI/INDEX',rows=300)
#df = quandl.get('NIKKEI/INDEX') #全日数取得
すごく簡単&無料です。
ただし、大量にデータがほしい場合は会員登録が必要です。
そのほかの注意点としては、データのフォーマットが結構まちまちです。
基本的にNIKKEI/INDEXの部分をほかのコードに書き換えれば、ほかの指標とか株価とかをとってこれますが、カラム名がまちまちですので注意する必要があります。
移動平均の表示と計算
移動平均の計算ですが、numpyを使うとすごく簡単。
1行で書けます。ループでぐるぐるさせる必要はありません。
何日の平均をだすかはwindowで指定できます。
ついでにグラフも出してみました。
実際はこんな感じ
#移動平均の計算
rm25 = df.rolling(window=25).mean()
rm10 = df.rolling(window=10).mean()
rm5 = df.rolling(window=5).mean()
#移動平均のグラフ描画
fig1=plt.figure(figsize=(20,10))
ax1=fig1.add_subplot(111)
plt.title("Price&rm")
ax1.plot(df[['Close Price']][100:],label="price")
ax1.plot(rm25[['Close Price']][100:],label="rm25")
ax1.plot(rm10[['Close Price']][100:],label="rm10")
ax1.plot(rm5[['Close Price']][100:],label="rm5")
plt.legend()
plt.tight_layout()
BB計算
続いてBBの計算です。
計算元となる平均をとる日数ですが、調べてみても具体的にどのぐらいにすればいいのかわかりませんでした。
大体の証券会社が20日で計算して表示しているようなので、とりあえず20日に設定してみました。
標準偏差の計算は.std()で可能です。
numpyは行列同士の四則演算が可能なのこちらもループをいちいち回す必要はなく
upper_band2 = rm + rstd * 2 lower_band2 = rm - rstd * 2
という感じ出かけるのが良いですね。
では実際のコードです。
これで、先ほどのFig1で示したグラフが生成されます。
#ボリンジャーバンドの計算
window_num=20 #移動平均を計算する日数
fig2=plt.figure(figsize=(20,10))
plt.title("BB")
ax2=fig2.add_subplot(111)
#標準偏差とBBの計算
rm = df[['Close Price']].rolling(window=window_num).mean()
rstd = df[['Close Price']].rolling(window=window_num).std()
upper_band1 = rm + rstd
lower_band1 = rm - rstd
upper_band2 = rm + rstd * 2
lower_band2 = rm - rstd * 2
upper_band3 = rm + rstd * 3
lower_band3 = rm - rstd * 3
ax2.plot(df[['Close Price']],label="price",color='blue')
ax2.plot(rm,label="rm",color="orange")
ax2.plot(upper_band1,label="upper1",color="#ff7f8f")
ax2.plot(lower_band1,label="lower1",color="#ff7f8f")
ax2.plot(upper_band2,label="upper2",color="#ce2143")
ax2.plot(lower_band2,label="lower2",color="#ce2143")
ax2.plot(upper_band3,label="upper3",color="red")
ax2.plot(lower_band3,label="lower3",color="red")
plt.legend()
plt.tight_layout()
確率の計算
では、BBのラインから外れる日数をカウントしてみます。
なんかもっとうまい書き方があるような気がするのですが…
#列をマージ
data = np.hstack([np.array(df[['Close Price']]), np.array(upper_band2),np.array(lower_band2), np.array(upper_band3),np.array(lower_band3)])
#欠損値を含むデータを削除
data = data[~np.isnan(data).any(axis=1)]
#シグマを超える日数
print('day:',len(data))
print('upper',np.count_nonzero(data[:,[0]]>data[:,[1]]))
print('lower',np.count_nonzero(data[:,[0]]<data[:,[2]]))
print('sigma2',(np.count_nonzero(data[:,[0]]>data[:,[1]])+np.count_nonzero(data[:,[0]]<data[:,[2]]))/len(data))
print('upper',np.count_nonzero(data[:,[0]]>data[:,[3]]))
print('lower',np.count_nonzero(data[:,[0]]<data[:,[4]]))
print('sigma3',(np.count_nonzero(data[:,[0]]>data[:,[3]])+np.count_nonzero(data[:,[0]]<data[:,[4]]))/len(data))
結果
取得日数300日(営業日281日)で計算してみたところ
day: 281 upper 6 lower 14 sigma2 0.0711743772241993 upper 0 lower 1 sigma3 0.0035587188612099642
σ3は1-0.997=0.003でほぼ一致しています
σ2については1-0.955=0.045 ですが大体あってるといっていいのでしょうか?微妙なところです。
取得日数を増やしてみます。
1950年からあるそうなので、コードを書き換えて実行してみた結果がこちら
day: 16702 upper 984 lower 801 sigma2 0.10687342833193629 upper 24 lower 51 sigma3 0.00449048018201413
え?σ2おおくね?10%?そんなもんなんでしょうかね?
カウント方法が間違っているとか、そもそも理論が違うのか?
これを正確とみるか不正確とみるか何とも言えません。
まぁσ3に関してはおおむねあってるという感じかなと思います。
ちなみに、Windowサイズを変えてみました
window=10
day: 16712 upper 481 lower 503 sigma2 0.05887984681665869 upper 0 lower 0 sigma3 0.0
window=30
day: 16692 upper 1218 lower 884 sigma2 0.12592858854541097 upper 32 lower 81 sigma3 0.006769710040738078
window=100
day: 16622 upper 1709 lower 849 sigma2 0.15389243171700157 upper 92 lower 109 sigma3 0.012092407652508724
windowサイズが大きくなうほどバンドから外れる傾向がありそうです。
20日ぐらいがちょうどよい感じに思えるので、20日にしているのには意味があるように思われます。





